Pierwiastek trzeciego stopnia, znany również jako pierwiastek sześcienny, to specyficzna operacja matematyczna. Jest to liczba, która pomnożona przez siebie trzy razy daje szukaną wartość. W matematyce oznaczamy go symbolem pierwiastka z cyfrą 3.
Obliczanie pierwiastka sześciennego może wydawać się trudne. Nie jest. Mamy kilka prostych metod. Można użyć kalkulatora, programu komputerowego lub obliczyć ręcznie. Każda metoda prowadzi do tego samego wyniku.
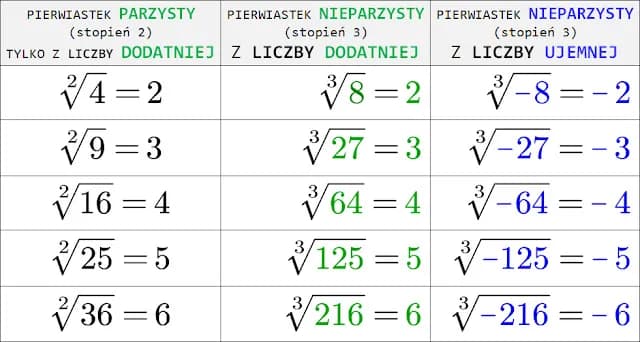
Najważniejsze informacje:- Pierwiastek sześcienny z liczby dodatniej zawsze daje liczbę dodatnią
- Pierwiastek sześcienny z liczby ujemnej daje liczbę ujemną
- Najłatwiej obliczyć go używając kalkulatora lub komputera
- Symbol pierwiastka trzeciego stopnia to ∛
- Przykład: pierwiastek sześcienny z 27 to 3, bo 3 × 3 × 3 = 27
- Zero jest pierwiastkiem sześciennym z zera
Czym jest pierwiastek trzeciego stopnia?
Pierwiastek trzeciego stopnia, zwany także sześciennym, to taka liczba, która pomnożona przez siebie trzy razy daje wynik równy liczbie pierwotnej. Dzięki niemu możemy łatwo określić wartość podstawową dla sześcianów liczb. To jedna z podstawowych operacji matematycznych, którą stosujemy przy rozwiązywaniu równań i zadań z geometrii przestrzennej.
Jak obliczyć pierwiastek sześcienny? To pytanie zadaje sobie wielu uczniów. Operacja ta może wydawać się skomplikowana, ale istnieje kilka prostych metod jej wykonania. Wystarczy poznać podstawowe zasady i wzory.
Metody obliczania pierwiastka trzeciego stopnia
Istnieją 4 główne sposoby na obliczanie pierwiastka sześciennego krok po kroku. Każda metoda ma swoje zalety i może być odpowiednia w różnych sytuacjach. Wybór właściwej metody zależy od dokładności, jakiej potrzebujemy.
- Metoda kalkulatorowa - najszybsza i najprostsza
- Metoda ręczna - pomocna w zrozumieniu procesu
- Metoda komputerowa - wykorzystująca programy matematyczne
- Metoda przybliżona - idealna dla szacunkowych wyników
Obliczanie pierwiastka sześciennego na kalkulatorze
Aby wyciągnąć pierwiastek trzeciego stopnia na kalkulatorze naukowym, wystarczy nacisnąć przycisk ∛ lub wybrać funkcję pierwiastka trzeciego stopnia. Następnie wprowadzamy liczbę i naciskamy znak równości.
Większość kalkulatorów graficznych posiada specjalny przycisk do obliczania pierwiastków dowolnego stopnia. W tym przypadku wybieramy trzeci stopień i wprowadzamy wartość.
Ręczne obliczanie pierwiastka trzeciego stopnia
Wzór na pierwiastek trzeciego stopnia można zastosować poprzez rozkład liczby na czynniki pierwsze. Kluczem jest grupowanie czynników po trzy.
Metoda ta wymaga znajomości tabliczki mnożenia i podstawowych zasad potęgowania. Jest szczególnie skuteczna przy liczbach, które są dokładnymi sześcianami.
| Liczba | Pierwiastek sześcienny |
| 8 | 2 |
| 27 | 3 |
| 64 | 4 |
| 125 | 5 |
Pierwiastek trzeciego stopnia z liczb ujemnych i dodatnich
Jak obliczyć pierwiastek trzeciego stopnia z liczby ujemnej? W przeciwieństwie do pierwiastka kwadratowego, pierwiastek sześcienny z liczby ujemnej zawsze istnieje i jest liczbą ujemną. Na przykład, pierwiastek sześcienny z -8 wynosi -2.
Dla liczb dodatnich pierwiastek sześcienny zawsze daje wynik dodatni. Jest to ważna własność, która pomaga w rozwiązywaniu równań trzeciego stopnia.
- Pierwiastek z liczby ujemnej jest liczbą ujemną
- Pierwiastek z liczby dodatniej jest liczbą dodatnią
- Pierwiastek z zera zawsze równa się zero
Przykłady obliczania pierwiastka sześciennego
Pierwiastek trzeciego stopnia przykłady pomogą lepiej zrozumieć proces obliczania. Poniżej znajdziesz rozwiązane zadania z różnymi typami liczb.
- Z liczby dodatniej: ∛27 = 3 (bo 3 × 3 × 3 = 27)
- Z liczby ujemnej: ∛(-8) = -2 (bo -2 × -2 × -2 = -8)
- Z ułamka: ∛(1/8) = 1/2 (bo 1/2 × 1/2 × 1/2 = 1/8)
- Z liczby całkowitej: ∛125 = 5 (bo 5 × 5 × 5 = 125)
- Z przybliżeniem: ∛100 ≈ 4,64 (dokładność do dwóch miejsc po przecinku)
Sprawdzanie poprawności wyniku
Najprostszym sposobem weryfikacji obliczania pierwiastka sześciennego jest podniesienie otrzymanego wyniku do trzeciej potęgi. Jeśli otrzymamy liczbę wyjściową, wynik jest poprawny.
Kalkulator pierwiastka sześciennego może pomóc w sprawdzeniu naszych obliczeń. Warto porównać wyniki otrzymane różnymi metodami.
| Najczęstszy błąd | Jak uniknąć? |
| Pomylenie znaku przy liczbach ujemnych | Zawsze pamiętaj o regule znaków |
| Niedokładne przybliżenia | Używaj kalkulatora naukowego |
| Błędy w potęgowaniu | Sprawdzaj wynik mnożąc trzykrotnie |
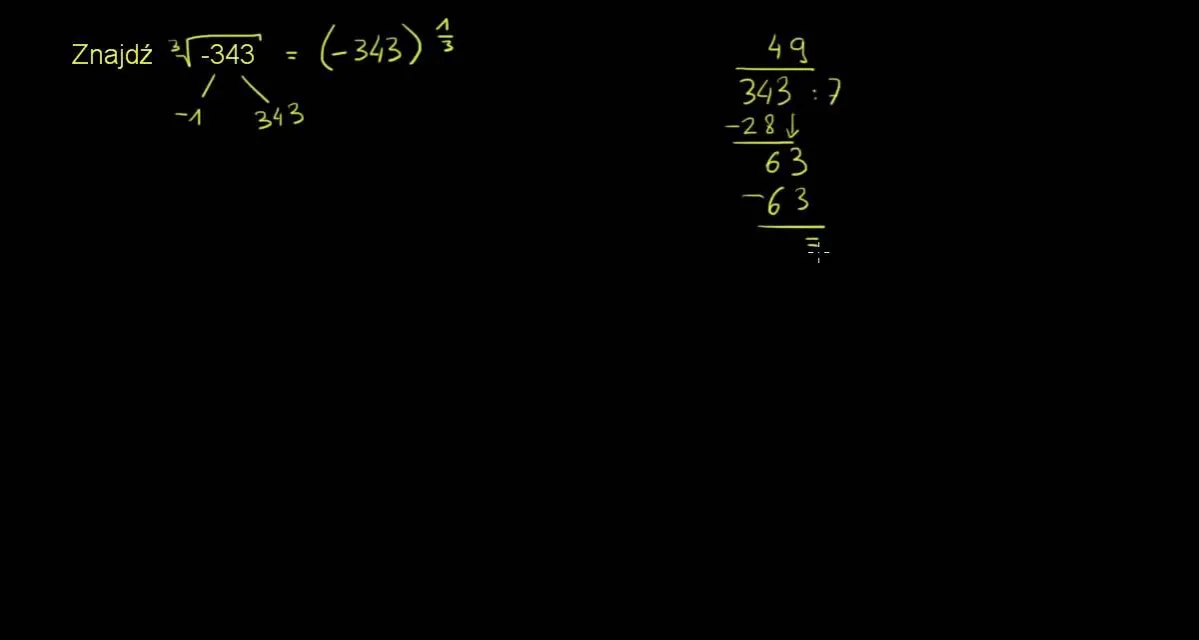
Zastosowanie pierwiastka trzeciego stopnia w praktyce
W życiu codziennym pierwiastek trzeciego stopnia pomaga w obliczaniu objętości i wymiarów przestrzennych. Jest niezbędny przy projektowaniu opakowań, gdy znamy objętość i potrzebujemy określić długość boku sześciennego pudełka. Znajduje też zastosowanie w obliczaniu wielkości pojemników o regularnych kształtach.
W nauce pierwiastki sześcienne są kluczowe dla fizyki i inżynierii. Pomagają w obliczeniach związanych z mechaniką kwantową, dynamiką płynów i wytrzymałością materiałów. W astronomii wykorzystuje się je do obliczania odległości między ciałami niebieskimi.
Technologia również korzysta z właściwości pierwiastka trzeciego stopnia. Programiści używają go w algorytmach graficznych i modelowaniu 3D. Jest nieodzowny w projektowaniu gier komputerowych i symulacjach fizycznych.
Co warto zapamiętać o pierwiastku trzeciego stopnia?
Pierwiastek trzeciego stopnia to operacja matematyczna, którą można wykonać na wiele sposobów. Najszybszą metodą jest użycie kalkulatora lub komputera, ale warto też znać sposób ręcznego obliczania, który pomaga lepiej zrozumieć proces. Pamiętaj, że każda liczba rzeczywista ma dokładnie jeden pierwiastek sześcienny.
Kluczową zaletą pierwiastka sześciennego jest jego uniwersalność - działa zarówno dla liczb dodatnich, jak i ujemnych. W przeciwieństwie do pierwiastka kwadratowego, pierwiastek trzeciego stopnia z liczby ujemnej zawsze istnieje i jest liczbą ujemną. To czyni go szczególnie przydatnym w zaawansowanych obliczeniach matematycznych i zastosowaniach praktycznych.
Znajomość podstawowych przykładów, takich jak ∛8=2 czy ∛27=3, znacznie ułatwia pracę z bardziej skomplikowanymi obliczeniami. Zawsze możesz sprawdzić swój wynik, podnosząc go do trzeciej potęgi - jeśli otrzymasz liczbę wyjściową, oznacza to, że obliczenia są poprawne. W praktyce obliczanie pierwiastka sześciennego znajduje zastosowanie w wielu dziedzinach: od projektowania opakowań po zaawansowane obliczenia w fizyce i inżynierii.