Liczba 9, następująca po 8 i poprzedzająca 10, to fascynujący element matematyki. Jest to liczba naturalna o wyjątkowych właściwościach. Jej szczególną cechą jest zasada podzielności - liczba jest podzielna przez 9, gdy suma jej cyfr również dzieli się przez 9. To sprawia, że jest ona niezwykle użyteczna w obliczeniach matematycznych.
W świecie nauki i kultury dziewiątka pełni istotną rolę. Jako liczba atomowa fluoru ma znaczenie w chemii, a w kulturze często symbolizuje duchowość i doskonałość.
Najważniejsze informacje:- Jest liczbą złożoną, będącą kwadratem liczby 3 (3²)
- Posiada tylko trzy dzielniki: 1, 3 i 9
- Ma unikalną właściwość dotyczącą sumy cyfr
- Występuje w różnych systemach liczbowych (binarnym jako 1001₂, ósemkowym jako 11₈)
- Ma znaczenie zarówno w nauce (liczba atomowa fluoru) jak i kulturze
Podstawowe działania matematyczne z liczbą 9
Liczba 9 to ostatnia cyfra jednocyfrowa w systemie dziesiętnym. Jest następnikiem liczby 8 i poprzednikiem liczby 10, co czyni ją wyjątkową w matematyce. Jej właściwości sprawiają, że działania z liczbą 9 są niezwykle interesujące.
W podstawowych obliczeniach z 9, cyfra ta wykazuje wiele ciekawych wzorów. Jest to liczba złożona, będąca kwadratem liczby 3, co daje jej szczególne miejsce w świecie matematyki. Ta właściwość czyni ją przydatną w wielu obliczeniach.
- Dodawanie: 9 + 9 = 18
- Odejmowanie: 9 - 5 = 4
- Mnożenie: 9 × 3 = 27
- Dzielenie: 9 ÷ 3 = 3
- Potęgowanie: 9² = 81
| Mnożenie | Wynik |
|---|---|
| 9 × 1 | 9 |
| 9 × 2 | 18 |
| 9 × 3 | 27 |
| 9 × 4 | 36 |
| 9 × 5 | 45 |
| 9 × 6 | 54 |
| 9 × 7 | 63 |
| 9 × 8 | 72 |
| 9 × 9 | 81 |
| 9 × 10 | 90 |
Dzielniki liczby 9 i ich znaczenie
Dzielniki liczby 9 matematyka to zbiór trzech liczb naturalnych: 1, 3 i 9. Ta stosunkowo niewielka liczba dzielników wynika z faktu, że 9 jest kwadratem liczby pierwszej 3. Każdy z tych dzielników ma szczególne znaczenie w rozkładzie liczby 9 na czynniki pierwsze.
Czytaj więcej: Rezystancja podłogi - kompletny poradnik z wymaganymi wartościami pomiarów
Jak sprawdzić podzielność przez 9?
Sprawdzanie podzielności przez 9 opiera się na prostej zasadzie sumowania cyfr. Jeśli suma wszystkich cyfr danej liczby jest podzielna przez 9, to cała liczba również jest podzielna przez 9.
Jak jest 9 to ile się równa matematyka w kontekście podzielności można sprawdzić błyskawicznie. Wystarczy zastosować regułę sumowania cyfr i sprawdzić końcowy wynik.
- 234: 2+3+4=9 (podzielna przez 9)
- 729: 7+2+9=18, 1+8=9 (podzielna przez 9)
- 999: 9+9+9=27, 2+7=9 (podzielna przez 9)
- 1989: 1+9+8+9=27, 2+7=9 (podzielna przez 9)
Właściwości matematyczne liczby 9
Liczba 9 właściwości matematyczne obejmują wiele unikalnych cech. Jest to największa jednocyfrowa liczba w systemie dziesiętnym.
W podstawowych obliczeniach z 9 zauważymy, że suma cyfr każdej wielokrotności 9 zawsze daje 9. Jest to jedyna liczba o takiej właściwości.
Cyfra 9 wykazuje też ciekawe wzory przy mnożeniu. Iloczyn 9 i dowolnej liczby naturalnej daje wynik, którego cyfry sumują się do 9.| System | Zapis |
|---|---|
| Dziesiętny | 9 |
| Binarny | 1001 |
| Ósemkowy | 11 |
| Szesnastkowy | 9 |
Zastosowanie liczby 9 w codziennych obliczeniach
Jak liczyć z liczbą 9 w praktycznych sytuacjach? Mnożenie przez 9 można uprościć dodając zero i odejmując liczbę wyjściową. W sklepie możemy użyć tego triku, gdy coś kosztuje 9 złotych.
Przy obliczaniu rabatów, liczba 9 właściwości matematyczne przydają się szczególnie. Gdy produkt kosztuje 99 złotych, łatwo obliczyć 10% rabatu, odejmując po prostu 9,90 zł. Wykorzystanie dziewiątki w cenach jest popularną strategią marketingową.W życiu codziennym 9 spotykamy wszędzie. Od numerów autobusów po godziny otwarcia sklepów, przykłady równań z 9 pojawiają się naturalnie.
Ciekawe wzory matematyczne z liczbą 9
Każda wielokrotność liczby 9 ma ciekawą właściwość: suma jej cyfr zawsze daje 9. Na przykład: 9×4=36, a 3+6=9.
Przy mnożeniu przez 9 liczb jednocyfrowych występuje sekwencja: pierwsza cyfra to zawsze o jeden mniej niż mnożnik, a druga to dopełnienie do 9.
Istnieje wiele fascynujących wzorów z dziewiątką. Na przykład: 123456789 × 9 = 1111111101, 12345679 × 9 = 111111111, a 98765432 × 9 = 888888888. Te wzory pokazują regularność i symetrię w matematyce.
Triki matematyczne z wykorzystaniem liczby 9
Szybkie mnożenie przez 9 można wykonać używając palców. Zginamy palec odpowiadający mnożnikowi, a liczba palców po lewej i prawej stronie daje wynik. Na przykład, dla 9×3 zginamy trzeci palec, mamy 2 palce po lewej i 7 po prawej, więc wynik to 27.
Inny trik to szybkie sprawdzanie wyników mnożenia przez 9. Jeśli suma cyfr wyniku nie daje 9, to gdzieś popełniliśmy błąd. To szczególnie przydatne przy sprawdzaniu obliczeń.
Te sztuczki działają zawsze. Można je wykorzystać do imponowania znajomym lub szybkiego liczenia w głowie.
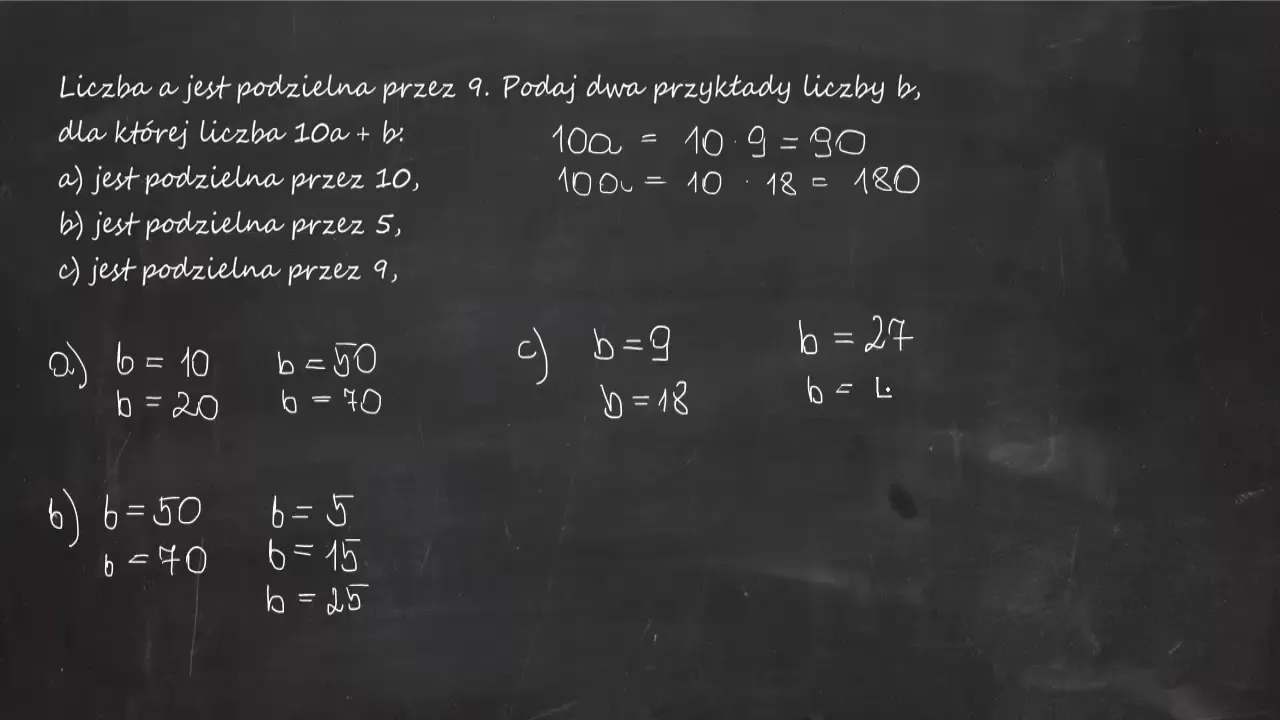
Ćwiczenia z liczbą 9 do samodzielnego rozwiązania
Praktyka czyni mistrza, szczególnie w matematyce. Poniżej znajdziesz zestaw zadań do przećwiczenia poznanych właściwości liczby 9.
- Zadanie 1: Oblicz 9876 ÷ 9 (Rozwiązanie: 1097, bo 1+0+9+7=17, 1+7=8+1=9)
- Zadanie 2: Znajdź sumę cyfr liczby 999999 (Rozwiązanie: 9+9+9+9+9+9=54, 5+4=9)
- Zadanie 3: Pomnóż 9 przez 12345 (Rozwiązanie: 111105)
- Zadanie 4: Sprawdź, czy liczba 8361 jest podzielna przez 9 (Rozwiązanie: 8+3+6+1=18, 1+8=9, więc tak)
- Zadanie 5: Oblicz 9³ (Rozwiązanie: 9×9×9=729, 7+2+9=18, 1+8=9)
Najważniejsze właściwości liczby 9 w praktyce
Liczba 9 wyróżnia się wyjątkowymi cechami matematycznymi, które czynią ją niezwykle użyteczną w codziennych obliczeniach. Jej najważniejszą właściwością jest zasada podzielności - suma cyfr każdej liczby podzielnej przez 9 zawsze daje w rezultacie 9.
Działania z liczbą 9 można znacznie uprościć dzięki sprytnym trikom matematycznym. Wystarczy zapamiętać, że przy mnożeniu pierwsza cyfra wyniku jest o jeden mniejsza od mnożnika, a druga to dopełnienie do 9. To sprawia, że obliczenia stają się szybsze i prostsze.
Praktyczne zastosowanie tych właściwości znajdziemy wszędzie - od sprawdzania rachunków po obliczanie rabatów. Trzy podstawowe dzielniki (1, 3 i 9) oraz reprezentacja w różnych systemach liczbowych pokazują, jak wszechstronna jest to liczba w świecie matematyki.