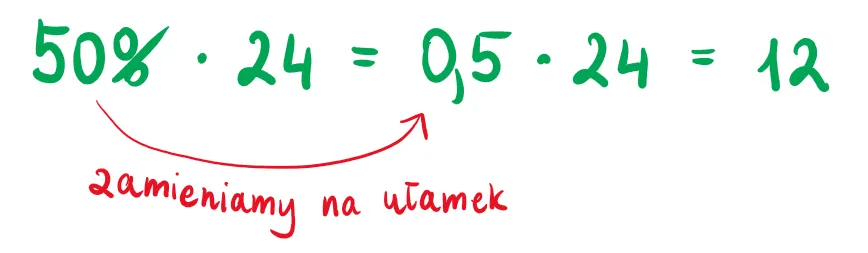Procenty są nieodłączną częścią naszego codziennego życia - od zakupów po finanse. Obliczanie procentów może wydawać się skomplikowane, ale w rzeczywistości opiera się na bardzo prostym wzorze matematycznym. To podstawowa umiejętność, która pomaga nam podejmować lepsze decyzje finansowe i rozumieć różne wartości liczbowe. Najważniejszym elementem jest zrozumienie, że procent to po prostu setna część całości.
Najważniejsze informacje:- Procenty można obliczyć dzieląc liczbę przez 100 i mnożąc przez wartość procentową
- Do obliczenia procentów służy wzór: (p/100) × n
- Istnieją różne metody obliczania - można wybrać tę najwygodniejszą
- Procenty można zamienić na ułamki dziesiętne, co ułatwia obliczenia
- Można również sprawdzić, jakim procentem jedna liczba jest względem drugiej
- Znajomość procentów jest kluczowa w codziennych sytuacjach, szczególnie w finansach
Podstawowy wzór na obliczanie procentów
Procenty to sposób wyrażania części całości w setnych częściach. Pozwalają one na proste porównywanie różnych wartości względem siebie. Jak policzyć ile to jest procent z danej liczby? Używamy do tego prostego wzoru matematycznego: wynik = (p/100) × n, gdzie p to procent, który chcemy obliczyć, a n to liczba wyjściowa.| Procent | Postać dziesiętna |
|---|---|
| 100% | 1,0 |
| 50% | 0,5 |
| 25% | 0,25 |
| 10% | 0,1 |
| 5% | 0,05 |
Co to znaczy policzyć procent z liczby
Jak obliczyć procent z liczby? To nic innego jak znalezienie części danej liczby. Jeśli mamy 200 zł i chcemy policzyć 25%, szukamy jednej czwartej tej kwoty. Spójrzmy na przykład: aby obliczyć 25% z 200 zł, mnożymy 200 przez 0,25 (25/100) i otrzymujemy 50 zł.
Krok po kroku jak obliczyć procent
Obliczanie procentów krok po kroku zaczyna się od zamiany procentu na ułamek dziesiętny. Następnie mnożymy otrzymaną liczbę przez wartość wyjściową.
Na przykład, aby obliczyć 30% z 400 zł, zamieniamy 30% na 0,3 i mnożymy przez 400, otrzymując 120 zł.
- Zapisz procent w postaci ułamka setnego
- Zamień ułamek na liczbę dziesiętną
- Pomnóż liczbę wyjściową przez otrzymaną liczbę dziesiętną
- Sprawdź, czy wynik jest logiczny
Czytaj więcej: Polskie koce wełniane! Dlaczego warto wybrać rodzimą produkcję?
Metody obliczania procentów w praktyce
Istnieją dwie główne metody jak wyliczyć procent z kwoty. Pierwsza polega na zamianie na ułamek dziesiętny, druga na mnożeniu i dzieleniu. Trzecia, mniej znana metoda, wykorzystuje proporcje.
Metoda przez zamianę na ułamek dziesiętny
Sposób obliczania procentów przez zamianę na ułamek dziesiętny jest najprostszy. Wystarczy zamienić procent na liczbę dziesiętną i pomnożyć przez wartość wyjściową.
Przykład: 15% z 80 zł = 0,15 × 80 = 12 zł
Metoda przez mnożenie i dzielenie
W tej metodzie najpierw mnożymy liczbę przez procent, a później dzielimy przez 100. Dla 35% z 400 zł obliczamy: (400 × 35) ÷ 100 = 140 zł.
Ta metoda jest szczególnie przydatna, gdy nie mamy pod ręką kalkulatora.
Przykłady obliczania procentów z życia codziennego
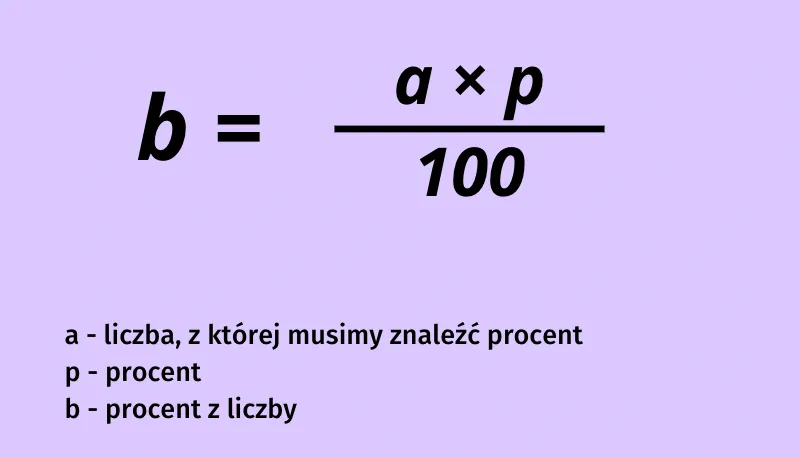
Codziennie spotykamy się z potrzebą obliczania procentów. Czy to podczas zakupów, w restauracji, czy przy sprawdzaniu zniżek. Jak policzyć ile to jest procent z danej liczby w praktycznych sytuacjach? Pokażemy to na konkretnych przykładach.
Obliczanie rabatów i promocji
Podczas wyprzedaży często spotykamy się z rabatami 30%. Dla produktu za 200 zł, rabat wyniesie: 200 × 0,3 = 60 zł. Końcowa cena to 140 zł.
Przy promocji "druga rzecz 50% taniej" dla dwóch produktów po 100 zł, rabat na drugi produkt to: 100 × 0,5 = 50 zł. Łącznie zapłacimy 150 zł.
Obliczanie napiwków w restauracji
Standardowy napiwek to często 10% rachunku. Dla rachunku 120 zł napiwek wyniesie: 120 × 0,1 = 12 zł.
Jeśli chcemy zostawić 15% napiwku przy rachunku 80 zł, obliczamy: 80 × 0,15 = 12 zł.
Użyteczne triki przy liczeniu procentów
Procent z liczby kalkulator nie zawsze jest pod ręką. Warto znać kilka prostych sztuczek. 10% to przesunięcie przecinka w lewo, 5% to połowa z 10%, a 1% to jedna dziesiąta z 10%.
Dla większych liczb warto rozbijać obliczenia na części. Na przykład 15% można obliczyć jako 10% + 5%.
- 10% = przesuń przecinek o jedno miejsce w lewo
- 5% = połowa z 10%
- 25% = połowa z 50% (czyli połowa z połowy)
- 1% = przesuń przecinek o dwa miejsca w lewo
- 75% = 50% + 25% (połowa + połowa z połowy)
Kluczowe zasady skutecznego obliczania procentów
Obliczanie procentów nie musi być trudne, gdy znamy podstawowy wzór (p/100) × n. To uniwersalne narzędzie pozwala nam wyliczyć procent z każdej liczby, niezależnie od kontekstu czy sytuacji.
Warto zapamiętać najprostsze triki - 10% to przesunięcie przecinka w lewo, 5% to połowa z 10%, a 25% to połowa z połowy. Te podstawowe metody obliczania procentów sprawdzają się szczególnie podczas codziennych zakupów czy wyliczania napiwków.
Najważniejsze to wybrać metodę, która najbardziej nam odpowiada - czy to przez zamianę na ułamek dziesiętny, czy przez mnożenie i dzielenie przez 100. Sposób obliczania procentów powinien być dla nas wygodny i intuicyjny, byśmy mogli szybko stosować go w praktyce.