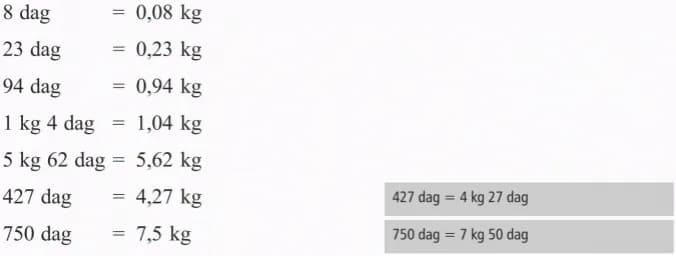Porównując liczby i określając, która jest większa, stosujemy odpowiednie działania matematyczne. Gdy pytamy "o ile większa", zawsze używamy odejmowania. Jest to kluczowa zasada w matematyce, która pozwala precyzyjnie określić różnicę między wartościami.
Wybór między dodawaniem a odejmowaniem zależy od celu naszych obliczeń. Dodawanie służy do łączenia wartości, podczas gdy odejmowanie pomaga znaleźć różnicę między nimi.
Najważniejsze informacje:- Aby sprawdzić o ile jedna liczba jest większa od drugiej, zawsze odejmujemy mniejszą od większej
- Dodawanie stosujemy tylko gdy chcemy uzyskać sumę wartości
- Przy porównywaniu dwóch liczb używamy wzoru: liczba większa - liczba mniejsza
- Wynik odejmowania pokazuje dokładną różnicę między porównywanymi wartościami
- W przypadku pytania "o ile więcej" zawsze wykonujemy odejmowanie
Kiedy używamy odejmowania przy porównywaniu liczb?
Jak obliczyć różnicę między liczbami? Matematyka daje nam jasną odpowiedź - zawsze używamy odejmowania. Porównywanie dwóch liczb odejmowanie to podstawowa zasada matematyczna, która pozwala precyzyjnie określić różnicę między wartościami.
Gdy pytamy "o ile większa jest jedna liczba od drugiej", kluczowe jest zastosowanie właściwego działania. Odejmowanie jest jedynym sposobem na znalezienie dokładnej różnicy. Zasada ta sprawdza się zarówno przy prostych, jak i bardziej złożonych obliczeniach.
Zasady odejmowania przy sprawdzaniu różnicy między wartościami
Obliczanie różnicy między wartościami opiera się na kilku podstawowych regułach. Pierwszą z nich jest zawsze odejmowanie mniejszej liczby od większej. Ta zasada gwarantuje otrzymanie poprawnego wyniku, który będzie miał praktyczne zastosowanie.
- Od większej liczby zawsze odejmujemy mniejszą
- Wynik pokazuje dokładną różnicę między porównywanymi wartościami
- Kolejność liczb ma znaczenie - zamiana miejscami da błędny wynik
- Przy porównywaniu stosujemy wzór: liczba większa - liczba mniejsza
Czytaj więcej: Ciśnienie atmosferyczne: Czym jest i jakie wartości osiąga?
Praktyczne przykłady porównywania liczb w życiu codziennym
Jak policzyć o ile więcej mamy pieniędzy czy innych wartości? Wystarczy zastosować odejmowanie w codziennych sytuacjach.
Jak sprawdzić która liczba jest większa i o ile? Najlepiej pokazać to na konkretnych przykładach.
| Sytuacja | Obliczenie | Interpretacja |
| Różnica w cenach | 150 zł - 120 zł = 30 zł | Produkt jest droższy o 30 zł |
| Różnica w temperaturze | 25°C - 18°C = 7°C | Temperatura wzrosła o 7 stopni |
| Różnica w wadze | 75 kg - 70 kg = 5 kg | Różnica wynosi 5 kilogramów |
Jak interpretować wynik odejmowania?
Wynik odejmowania zawsze pokazuje konkretną różnicę między dwiema wartościami. Jest to liczba, która mówi nam, o ile jednostek jedna wartość przewyższa drugą.
Interpretacja wyniku zależy od kontekstu zadania. Możemy mówić o różnicy w złotówkach, kilogramach, stopniach czy innych jednostkach.
Najczęstsze błędy przy porównywaniu liczb

Pierwszym częstym błędem jest odejmowanie większej liczby od mniejszej. Prowadzi to do otrzymania wyniku ujemnego, który nie pokazuje rzeczywistej różnicy.
Drugim popularnym błędem jest próba użycia dodawania zamiast odejmowania. To działanie nie pozwala określić różnicy między wartościami.
- Zawsze sprawdzaj, która liczba jest większa przed wykonaniem działania
- Używaj tylko odejmowania do porównywania wartości
- Zwracaj uwagę na jednostki przy porównywaniu wartości
Metody sprawdzania poprawności obliczeń
Najprostszą metodą weryfikacji wyniku jest wykonanie działania odwrotnego. Dodając do mniejszej liczby otrzymaną różnicę, powinniśmy uzyskać liczbę większą. Dzięki temu szybko sprawdzimy poprawność naszych obliczeń.
Warto też oszacować wynik przed wykonaniem działania. Przybliżone wartości pomogą zauważyć ewentualne błędy w obliczeniach. Możemy też użyć kalkulatora do potwierdzenia naszych ręcznych obliczeń.
Dlaczego nie należy dodawać liczb przy sprawdzaniu różnicy?
Dodawanie nie pozwala określić różnicy między wartościami. Suma dwóch liczb to zupełnie inna informacja niż różnica między nimi.
Tylko odejmowanie pokazuje rzeczywistą różnicę między liczbami. "Jak jest o ile większa to dodajemy czy odejmujemy" - odpowiedź jest jednoznaczna: zawsze odejmujemy.
Najważniejsze zasady porównywania liczb w praktyce
Kluczem do prawidłowego porównywania liczb jest zawsze używanie odejmowania, nigdy dodawania. Gdy pytamy o różnicę między wartościami, musimy pamiętać o podstawowej zasadzie: większa liczba minus mniejsza liczba.
Unikanie błędów jest możliwe dzięki przestrzeganiu prostej kolejności działań. Najpierw sprawdzamy, która liczba jest większa, następnie od niej odejmujemy mniejszą wartość. Wynik zawsze pokazuje nam dokładną różnicę między porównywanymi wartościami.
W codziennym życiu stosowanie odejmowania do porównywania wartości ma szerokie zastosowanie - od sprawdzania różnic w cenach, przez porównywanie temperatur, aż po obliczanie różnic w wadze. Poprawność obliczeń możemy łatwo zweryfikować, dodając do mniejszej liczby otrzymaną różnicę.